Comparação dos tipos de cabeça: Hemi, SE, F&D e Flat
Upload Time:
Dec 31, 2024
Uma concha cilíndrica é fabricada usando material SA-516 Grade 70 de 0,500 polegadas de espessura, que é avaliado para 20.000 psi a 100 ° F. A concha é rolada para um diâmetro externo (OD) de 48 polegadas, resultando em um diâmetro interno (ID) de 47 polegadas. O cilindro, juntamente com as costuras que o ligam a qualquer cabeça ligada, é submetido a uma inspeção radiográfica completa. Nenhuma concessão de corrosão foi considerada no projeto. De acordo com a ASME Seção VIII, Divisão 1, a pressão de projeto calculada para este cilindro é de 420 psi.
Vasos de pressão geralmente usam quatro tipos de cabeças: Hemisférico (Hemi), Semi-Elíptico (SE), Flanged e Dished (F & amp; D) e Plano. Nesta análise, cada cabeça é considerada como sendo ligada a uma concha cilíndrica, com seus diâmetros internos (ID) correspondentes ao cilindro' s. A espessura da parede para cada cabeça é ajustada para atender ao cilindro' s pressão de projeto de 420 psi. Os cálculos detalhados podem ser acessados através do link fornecido abaixo.
Os resultados incluem a espessura da parede, altura total, volume interno e peso de uma única cabeça, considerando quaisquer flanges retas quando aplicáveis:
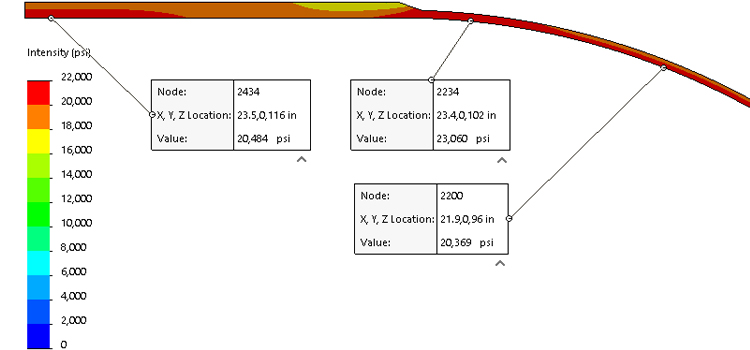
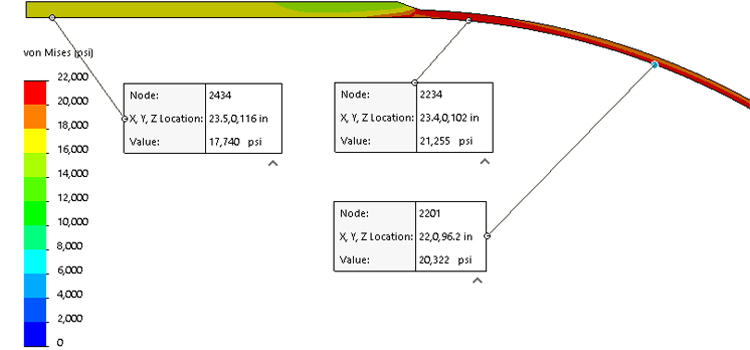
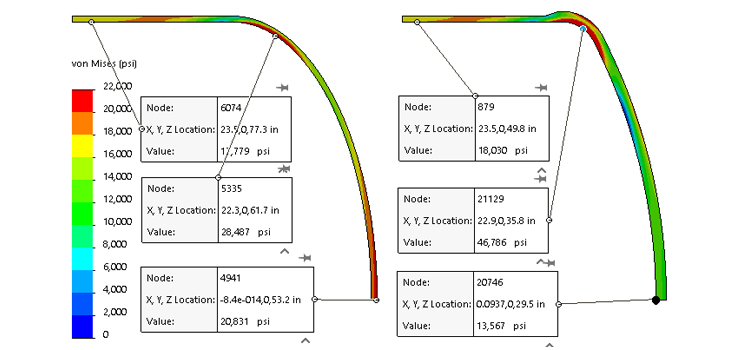
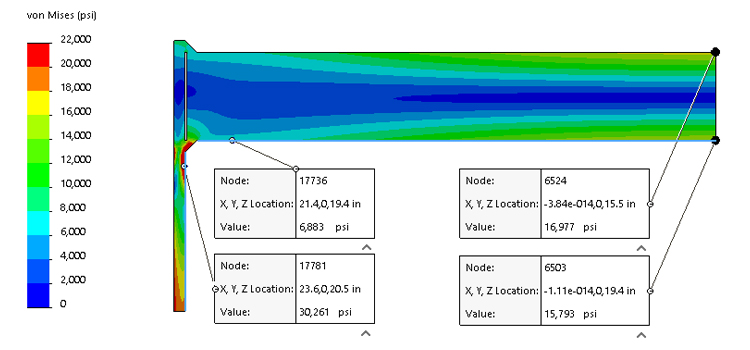
A cabeça hemisférica apresenta uma geometria radial simples, com uma profundidade igual a metade de seu diâmetro. Para uma cabeça com um diâmetro interno de 47" (ID), a espessura da parede necessária é de 0,2474", que é cerca de metade da espessura da concha cilíndrica. Como a cabeça é mais fina do que a concha, um cónico 3:1 padrão conforme o código ASME é aplicado na transição. Este cónico faz parte da cabeça mais forte, enquanto a concha cilíndrica mantém toda a sua espessura ao longo da seção reta para a força. Cabeças hemisféricas geralmente não são formadas a partir de uma placa plana, mas são fabricadas a partir de segmentos soldados. Isso os torna o tipo de cabeça mais fino, mas às vezes o mais caro. Eles são comumente usados em aplicações de alta pressão ou de grande diâmetro onde a poupança de material é crítica. Além disso, duas cabeças hemisféricas unidas de volta a volta criam uma esfera de armazenamento, a forma mais eficiente para armazenamento pressurizado. A cabeça semi-elíptica tem uma forma elíptica, com a relação mais comum sendo 2:1, onde a largura da elipse é o dobro da sua profundidade. Na prática, os fabricantes muitas vezes usam três raios para aproximar a elipse: um grande raio na coroa, um pequeno raio na borda externa e um raio intermediário no meio. As regras do código ASME especificam o quão perto a cabeça fabricada deve aproximar-se de uma elipse verdadeira. Para uma cabeça 2:1 SE, a profundidade é de um quarto do diâmetro, tornando-a mais rasa do que uma cabeça hemisférica, mas mais profunda do que cabeças flanjadas e placadas (F & amp; D) ou planas. Esta cabeça pode ser formada a partir de uma placa plana, tornando-a uma das opções mais econômicas para vasos de baixa pressão. Embora menos eficiente do que a cabeça hemisférica no manuseio de tensões, cabeças SE exigem um pouco mais de espessura. Por exemplo, a espessura necessária para uma cabeça SE 2:1 neste caso é de 0,4947", ligeiramente menor que a espessura da concha cilíndrica de 0,500". Cabeças com flanges e placas são comumente usadas em aplicações de pressão moderada onde minimizar a altura é importante. Neste design, o raio da coroa é igual ao diâmetro externo do cilindro (48"), e o articular tem um raio apertado de 2.973". Isso resulta em uma cabeça com um perfil mais baixo do que a cabeça semi-elíptica. No entanto, o raio apertado do articular induz altas tensões de formação, exigindo tratamento térmico pós-formação para alívio do estresse. O F& Cabeça D requer uma parede mais espessa do que o cilindro, com uma espessura necessária de 0,8901". Um cónico padrão de 3:1 na seção reta da flange da cabeça lida com a transição, pois a porção da flange só precisa corresponder à espessura de 0,500" do cilindro. Para pressões de até 420 psi, cabeças SE são tipicamente preferidas, a menos que restrições de altura dictem o contrário. A cabeça plana é o design menos eficiente, pois resiste à pressão principalmente através da dobra, o que resulta em requisitos de material significativamente maiores. Neste caso, a espessura necessária é de 3,9120", tornando-a muito mais pesada do que outros tipos de cabeça. Cabeças planas são geralmente usadas quando uma superfície interna plana é essencial para o processo. Vários métodos alternativos reduzem o peso das cabeças planas: As fórmulas de código ASME VIII-1 para cilindros e cabeças hemisféricas são fáceis de derivar. Para o cilindro de espessura de 0,5", a tensão calculada atinge o limite de projeto de 20.000 psi. FEA usando análise de estresse Tresca produz um valor ligeiramente maior de 20.484 psi. Da mesma forma, a cabeça hemisférica de 0,2474" de espessura alcança uma tensão Tresca de 20.364 psi, correspondendo estreitamente ao valor alvo. Estes resultados confirmam que tanto o cilindro quanto a cabeça hemisférica atendem aos requisitos de tensão do projeto com excelente precisão. A tensão na zona de descontinuidade onde a cabeça encontra a concha é maior, atingindo 23.060 psi. As regras de código ASME Seção VIII, Divisão 2 (VIII-2) permitem aumentos localizados de tensão em pequenas distâncias, desde que permaneçam dentro de limites especificados. Neste caso, os níveis de estresse são considerados aceitáveis. Em contraste, as regras da ASME Seção VIII, Divisão 1 (VIII-1) não levam em conta essas tensões localizadas além de exigir uma redução de 3:1. No entanto, a experiência prática mostra que essa abordagem é confiável. A análise de tensão da Tresca mostra uma estreita correlação entre os valores de tensão previstos pelas fórmulas de código VIII-1 e aqueles obtidos através da análise de elementos finitos (FEA) sob as diretrizes VIII-2 para o cilindro e a cabeça hemisférica. No entanto, o ASME VIII-2 passou do uso do critério Tresca (estresse P1-P3) para a formulação de estresse de von Mises, fornecendo uma representação mais abrangente do comportamento de estresse. A tensão de von Mises no cilindro e na cabeça hemi – a tensão do cilindro está agora 12% abaixo do código VIII-1 Seja cauteloso usando FEA para o projeto desses dois tipos de cabeça, porque as tensões dos articulares estão em tensão na direção longitudinal (ao longo do comprimento da concha), mas podem ser compressivas na direção radial. O articular dessas cabeças pode se fechar se for feito muito fino. Como os métodos FEA são mais comumente usados, esperamos que F& D espessuras da cabeça (para cabeças mais finas de grande diâmetro) serão maiores. Nós não esperamos que os projetos de cabeça SE mudem muito. & nbsp; Estresse em cabeças planas As fórmulas VIII-1 para cabeças planas resultam em cabeças que têm tensões de seção central calculadas pela FEA muito menores do que as regras do código permitem. nbsp; A cabeça plana está em dobra, que tem tensões permitidas de 1,5x membrana, ou 30.000 psi neste caso. nbsp; O estresse central real é metade disso. & nbsp; As regras do código são mais focadas na transição de cabeça para shell, onde uma cabeça superconstruída mantém a transição segura. nbsp; À medida que os designers obtêm mais liberdade para usar métodos VIII-2 FEA no design de cabeça plana, sempre que possível, as cabeças serão mais finas em todo o redondo, com mais espessura no centro do que as bordas. Essas cabeças mais finas terão mais rotação na cabeça para a junção da concha, exigindo que o designer dê a essa área muito merecida atenção. À medida que o uso de FEA se torna mais comum, esperamos que as espessuras da cabeça plana diminuam.Cabeça Espessura [ em ] Altura externa [ em ] Volume [ US gal ] Peso [ lbs ] Cilindro, 24" comprido 0.5 24 180.25 506.7 Hemi 0.2474 23.75 117.7 245.5 SE * 0.4947 13.74 70.1 397.3 F& D * 0.8901 10.29 47.7 602.9 Plana 3.9120 3.91 0 1920.8 * Incluindo a flange reta de 1 ½ " 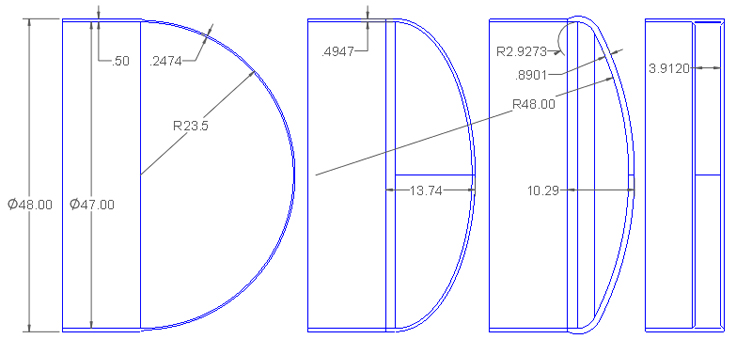
Cabeça Hemisférica (Hemi)
Cabeça Semi-Elíptica (SE)
Cabeça Flanged e Dished (F&D)
Cabeça plana
Análise de estresse com análise de elementos finitos (FEA)
Cilindro e Hemi Cabeça Tresca Stresses
Cilindro e cabeça Hemi von Mises Stresses
Relevant News








